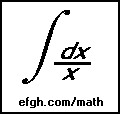Source: http://www.efgh.com/math/impossible.htm

Филип Ј. Ерделски (Philip J. Erdelsky)

Првпат објавена во Д-р Добб е весник мај 1987 година

 

Секој кој е сведок на огромните подобрувања во компјутерите во последните 40 години може да добие впечаток дека компјутерите на крајот ќе можат да го решат секој добро дефиниран проблем. Напредокот во разбирањето на јазикот и другите форми на вештачка интелигенција е разочарувачки, но човечкиот јазик е полн со двосмислености, така што тоа не е добро дефиниран проблем. Шах, од друга страна, е многу добро дефиниран. Иако некогаш се сметаше за олицетворение на интелегентната активност, компјутерите сега можат да играат подобро отколку сите, освен неколку човечки играчи.

Некои проблеми, иако добро дефинирани, се премногу големи за да се решат во разумен рок дури и на нашите најголеми компјутери. Но, сигурно, ако компјутерот може да биде ослободен од сите ограничувања на време и меморија, не можеше да реши некој добро дефиниран проблем?

Изненадувачки одговор на ова прашање, кој беше познат на математичарите дури и пред да се изградат првите вистински компјутери, не е. Има некои работи што никој друг не може да ги направи, бидејќи може да се докаже дека не постојат алгоритми за нивно извршување – исто како што нема начин да се постави круг со компас и исправен чекор.

Овие работи не се само математички куриозитети. Тоа се работи кои програмерите би сакале да ги направат нивните компјутери за нив и работите што добавувачите на алатки за развој на софтвер би сакале да ги вклучат во нивните дебагери. Наставните програми за компјутерски науки обично вклучуваат предмет на неизвесни функции, но програмерите кои не се компјутерски науки специјалност понекогаш бараат невозможно без да го реализираат.

Алан Тјуринг во 1935 година прашал дали постои метод со кој компјутерската програма може да одреди дали ќе прекине некоја друга компјутерска програма. Ова е познатиот “проблем за запирање”. Тјуринг покажа дека нема решение.

Дебагерот со оваа способност сигурно ќе биде корисен. Неуспехот да се запре нормално е честа форма на неуспех на програмата. Згора на тоа, дебагерот може да се примени последователно на делови од неуспешната програма за да се изолира делот кој е обесен.

Не е очигледно дека таков дебагер е невозможен. Се разбира, дебагерот не може само да ја чекори програмата за да види дали ќе застане. Ако програмата не застане, дебагерот може да работи засекогаш без да утврди дека ова е случај. Или тоа може да се откаже исто како што програмата ќе заврши, како што понекогаш прават човечките програмери. Во одреден момент, дебагерот ќе мора да може да каже: “Аха! Оваа јамка е бесконечна!” Се чини дека како умно напишан дебагер, кој има сите алатки на модерните јазици на високо ниво, може да го стори тоа.

Невозможното доказ се базира на следниот аргумент. Ако имате дебагер што може да го реши проблемот за запирање, со оглед на неограничено време и меморија, тогаш можете да го користите истиот код за да го направите дебагерот да прави други работи, од кои некои се самопротивидни и оттаму невозможни.

Посебниот компјутерски јазик не е важен. Ако можете да го решите проблемот на запирање на еден јазик, можете да го решите за друг. Само користете компајлер или друга програма за преведување пред да го решите проблемот со запирање. Забележете дека преведувањето на програма на асемблерски јазик на повисоко ниво е многу лесно, иако објектната програма е неизбежна. Целта, сепак, е да покаже дека решението за проблемот на запирање е невозможно, а не само неефикасно.

Самиот Тјуринг предложил минимална машина што се нарекува машина Тјуринг. Неговото сеќавање требаше да биде бесконечно долго, но само еден бит широк, а машината имаше само секвенцијален пристап до него, како и со лента. Програмскиот јазик во суштина беше дијаграм со само неколку основни команди. Сепак, Тјуринг покажа дека неговата машина можела да имитира било која друга машина, имајќи доволно време и соодветна програма. Ваквата конструкција не е неопходна за нашите цели – можете да замислите дека компјутерот е програмиран на некој познат јазик на високо ниво.

Сега разгледајте го проблемот за одредување дали една програма може да испечати одреден стринг S (со или без друг излез). Ако можете да го решите проблемот со запирање, можете да го решите овој проблем. Само заменете ја секоја изјава за печатење во програмата со рутина која не го испраќа излезот до печатачот, туку води сметка за излезот и застанува кога се појавува низата S. Потоа, за да ја задржите програмата од запирање од која било друга причина, заменете ги сите застојни изјави во програмата со бескрајни јамки. Потоа решавајте го проблемот за запирање на резултатот.

Таквата програма би била корисна сама по себе, бидејќи многу грешки во време на извршување создаваат специфични пораки, и би било корисно однапред да се предвиди дека таквите грешки ќе се појават.

Бидејќи ова се однесува на било која низа S, исто така можете да одредите дали програмата отпечатоци копија од себе. Ова не е толку љубопитно што се појавува на прв поглед. Лесно е да се напише програма со 1.000 карактери која ги отпечатоци сите комбинации од 1.000 карактери, вклучувајќи ја и самата. Всушност, 1.000 карактери е веројатно преценет од бројот на знаци што се бараат на повеќето јазици на високо ниво.

Сега можете да напишете програма за да ги направите следните работи. Прво, генерирајте, еден по еден, сите можни програми. Најлесен начин да го направите ова е да ги генерирате сите жици и да ги проверите секој за да видите дали е програма. Составувачите го прават ова кога проверуваат синтакса. Потоа проверете ја секоја програма за да видите дали таа печати копија од себе. Конечно, отпечатете копија од секоја програма која не печати копија од себе.

Оваа програма, во процесот на генерирање на сите програми, на крајот ќе се генерира. Дали испечати копија од себе? Ако го стори тоа, го крши правилото со печатење на копија од програма која отпечатоци копија од себе. Ако не, тоа го крши правилото со тоа што не успеа да испечати копија од програма што не печати копија од себе. Оваа фатална контрадикција докажува дека проблемот на запирање нема решение.

Ова може да го препознаете како парадокс на Расел (збир од сите множества кои не се самите себеси) или како парадокс на бербер (бербер кој го бричи секој човек кој не се бричи).

Секој проблем што дебагерот може да го претвори во проблем за запирање, како што е проблемот со низа излез, е подеднакво нерешлив. Некои други очигледни примери се:

1. утврдување на тоа дали програмата ќе достигне одреден момент (Ада програмери: тоа е причината зошто PROGRAM_ERROR мора да биде грешка на кандидира време, а не грешка на компајлирање време)
2. утврдување дали една променлива се иницијализира пред да се користи
3. утврдување дали даден сегмент од кодот е недостапен и никогаш нема да биде извршена
4. утврдување на тоа дали двете програми го прават истото

Се разбира, дебагерот или компајлерот понекогаш може да предвиди такви грешки – на пример, понекогаш недостапен код понекогаш може да се идентификува во времето на компајлирање. Но универзални решенија за ваквите проблеми не постојат.

Неможноста за утврдување на тоа дали двете програми го прават истото значи дека секогаш е можно да го порази на одреден вид на тројански коњ. На предавањето во печатени во Известувањата на АЦМ (август 1984), Кен Томпсон тврдеше дека тој може да се стави тројански коњ во C компајлер кој ќе погрешно компајлирање за најава изјава да му овозможи пристап до било кој систем Unix состави со тоа, и тоа ќе погрешно компајлирање на C компајлер да вметнете копија од себе. Самата тројански коњ не ќе се појави во изворниот код за компајлер C. Во писмо до уредникот, Стив Драпер напомене дека како тројански коњ може да биде поразен од страна на парафразирање на C компајлер (пишување на различни кодот што го прави истото), а потоа рекомпајлирање. Не тројански коњ може да неизоставно го признае парафразирани програми – тоа постои секогаш парафраза дека ќе го порази тројански коњ.

Мое мислење во врска со ова прашање е дека, освен ако тројанскиот коњ не е вешто напишан, повеќето парафрази би го поразиле, и всушност тоа веројатно би било поразено на крајот со нормално одржување на софтверот. Секој тројански коњ кој е доволно паметен да ги препознае повеќето парафрази, веројатно би бил многу поголем од остатокот од компајлерот на C. Никогаш нема да го достигнете тоа низ портите.

Заштитниот проблем е тесно поврзан со два други проблеми, кои ги поставуваше математичарот Дејвид Хилберт во 1900 година. Дали има формален доказ или непропустливост за секоја математичка изјава? Дали постои алгоритам за да се најдат докази?

Првото прашање беше одговорено негативно од Курт Гедел во 1931 година. Доказот на Гедел беше комплексен, но ако прифатите нерешливоста на проблемот на запирање, може да се докаже едноставно. Дали одредена програма престанува е математичка изјава. Всушност, многу математички теореми се веќе посебни случаи на проблемот на запирање, затоа што можете да напишете програма за да барате контрагенери и да застанете кога ќе ја најдат. Теорема е еквивалентна на тврдењето дека програмата никогаш не запре.

Ако секогаш постоеше формален доказ или отфрлање на тврдењето дека програмата се прекинува, тогаш можете едноставно да ги генерирате сите докази (повеќе или помалку, како што програмата опишана порано ги генерирала сите програми) додека не најдете доказ или непристојност. Тоа ќе го реши проблемот со запирање. Бидејќи проблемот за застанување е генерално нерастворлив, мора да има најмалку една математичка изјава од ваков вид која е неопределена – односно, таа не може да биде формално докажана или негирана.

Ова покажува дека е невозможно воопшто да докаже дека програмата функционира. Може да се докажат одредени програми или ограничени класи на програми за изведување на одредени работи, но не постои начин да се направи ова за секоја програма.

Со оглед на тоа што некои математички изјави се неразбирливи, дали постои програма, “програма за одлучност”, која може да покаже дали било каква математичка изјава е одлучлива, дури и без да се одлучи дали е точна или неточна? Како што можеше да се претпостави од тонот на оваа статија, одговорот е повторно не. Ако имате програма за одлучување, можете да ја преземете секоја програма и да прашувате дали ќе престане. Потоа примени ја програмата за одлучување на ова прашање. Ако прашањето е разумно, пребарувањето на сите докази ќе го докаже или ќе го оспори. Ако прашањето е неопределено, тогаш програмата никогаш не се прекинува; во спротивно, можете да докажете дека ќе застане со едноставно извршување додека не запре.

Затоа, програмите за докажување на теоремите, колку и да се успешни тие можат да бидат во ограничени области, никогаш не можат да докажат сè. Некои работи секогаш мора да останат надвор од нивното разбирање.

Овие аргументи не се ригорозни во математичката смисла, бидејќи премногу се изоставени. Голем дел од делата на Тјуринг и Гедел вклучувале формализација на концептите на “пресметување” и “доказ” до точката во која нивните аргументи би биле прифатени од страна на математичарите.

Можеби веќе сте забележале една премолчена претпоставка која не одговара на реалноста. Програмите не се ограничени со ограничувања на меморијата. Ако некоја програма има ограничување на меморијата, тогаш проблемот за запирање може теоретски да се реши – но само со програма со многу поголема меморија.

Ова е како може да се направи. Програма со ограничување на меморијата има само ограничен број на состојби. Дебагерот може да го поправа, следејќи ги состојбите што ги окупира. Ако ја зазема истата состојба двапати пред да прекине, таа ќе го повторува истиот редослед на држави на неодредено време и никогаш нема да запре.

За да го направите ова, дебагерот има потреба од доволно меморија за да ги следи кои состојби програмата ја окупирала. Само еден бит е потребен за секоја можна состојба, но бројот на можни состојби за дури едноставна програма е навистина преголем. Секоја комбинација на битови во меморијата е друга состојба. Оттука, програмата со само 1.024 бајти на меморија има најмалку 2^(1024×8) состојби поради само конфигурација на меморија, да не кажуваат ништо за знамињата и регистрите. Овој број на флип-flops не би се вклопил во целиот познат универзум. Затоа може да се каже дека проблемот на запирање нема решение дури и во овој случај.

Тогаш треба да биде јасно дека дефинитивно има одредени ограничувања на она што вештачката интелигенција може да го постигне и дека работниците на математичарите и програмерите никогаш не можат целосно да се автоматизираат. (Ова е голема утеха за мене, бидејќи сум математичар и програмер.

Сепак, совршени решенија се невозможни. Сеуште може да се тврди, и некои тврдат дека програмите за вештачка интелигенција на крајот ќе можат да го решат секој проблем што човечкиот ум може да го реши, со најмалку иста стапка на успех. И ако единствениот услов е практични решенија, а не совршени решенија, тогаш многу интересни, но теоретски нерешливи проблеми може да се решат.