Source: http://galileoandeinstein.physics.virginia.edu/lectures/gkastr1.html
Мајкл Фаулер (Michael Fowler)
Универзитетот во Вирџинија Одделот за физика
UVa Physics Department
Во ова предавање, ќе покажеме како Грците ги направија првите вистински мерења на астрономските растојанија: големината на земјата и растојанието до месечината, точно утврдени и растојанието до сонцето, каде што нивната најдобра проценка е кратко фактор на два.
Колку е голема Земјата?
Првиот разумно добар мерење на големината на земјата е направено од страна на Ератостен, грчки, кој живееше во Александрија, Египет, во третиот век пред нашата ера Тој знаеше дека далеку на југ, во градот на Сиен (денешен Асуан, таму каде што е сега огромна брана на Нил) имаше еден длабок бунар и на пладне на 21 јуни, на сончева светлина се гледа надвор од вода далеку во ова добро, нешто што се случило на ниту еден друг ден од годината. Поентата е дека сонцето е точно вертикално над глава во тоа време, и во ниеден друг пат во годината. Ератостен знаел дека сонцето никогаш не беше вертикално над глава во Александрија, најблиску што го добив беше на 21 јуни, кога тоа е надвор од агол тој резултат да биде околу 7,2 степени, со мерење на сенката на вертикална стап.
Растојанието од Александрија до Сиен беше измерено на 5.000 стадиуми (стадиум од 500 метри), речиси точно југ. Од ова, и разликата во аголот на сончевата светлина во пладне на 21 јуни, Ератостен успеа да сфати колку далеку би било да одат целосно околу земјата.
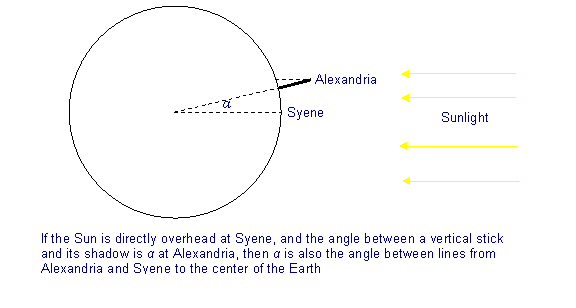
Се разбира, Ератостен целосно призната дека Земјата е сферична форма, и дека “вертикално надолу” каде било на површината само значи насока кон центарот од таа точка.Така две вертикални шипки, една во Александрија и еден на Сиен, не беа навистина паралелно. Од друга страна, зраците на сончевата светлина паѓа во две места беа паралелно. Затоа, ако сончевите зраци се паралелни со вертикалната стап во Сиен (па тоа немаше сенка) аголот тие го направија со стап во Александрија беше иста како и колку далеку околу Земјата, и во степени, Александрија беше од Сиен.
Според грчкиот историчар Клемедес, Ератостен ги мери аголот помеѓу сончевата светлина и стапот во пладне во средната летна година во Александрија да биде 7,2 степени, или еден петесетти полн круг. Евидентно е да се извлече слика за тоа дека ова е истиот агол како оној меѓу Александрија и Сиен како што се гледа од центарот на земјата, така што растојанието меѓу нив, 5.000 стадиуми, мора да биде една петтина од растојанието околу земјата, која е еднаква на 250.000 стадиуми, околу 23.300 милји. Точниот одговор е околу 25.000 милји, и, всушност, Ератостен можеби бил поблизок отколку што го наведовме овде — ние не сме сосема сигурни колку е преодна стада, а некои научници тврдат дека е околу 520 метри, што би го ставило уште поблиску.
Колку висока е Месечината?
Како да почнеме да ја мериме растојанието од Земјата до Месечината? Една очигледна мисла е да се измери аголот на Месечината од два града, далеку од исто време, и да се конструира сличен триаголник, како што е Талес, мерејќи ја растојанието од бродот на море. За жал, разликата во аголот од две точки неколку стотици милји е премногу мала за да може да се измери со техниките што се користат во тој момент, така што методот нема да функционира.
Сепак, грчки астрономи, почнувајќи со Аристарх од Самос (310-230 п.н.е., приближно) излезе со еден умен метод за наоѓање на оддалеченост на Месечината, со внимателно набљудување на затемнувањето на Месечината, што се случува кога земјата штитови на Месечината од светлината на сонцето.
За краток филм илустрирање на затемнувањето на Месечината, кликнете тука!
За подобро да се визуелизира на затемнувањето на Месечината, замислете држи до една четвртина (со дијаметар од околу еден инч) на растојание каде што само го блокира сончевите зраци од едното око. Се разбира дека не треба да се обидат ова-ти ќе оштетување на окото! Можете да ја обидат со полна месечина, која се случува да биде иста привидна големина на небото како сонце. Излегува дека правото растојание е околу девет нозете подалеку, или 108 инчи. Ако квартал е подалеку од тоа, тоа не е доволно голема за да ги блокирате сите сончева светлина. Ако тоа е поблиску од 108 инчи, тоа целосно ќе го блокира сончевата светлина од некои мали кружни област, која постепено се зголемува во големина се движи кон квартал. Така, дел од просторот каде што сончевата светлина е целосно блокирани е конусна, како долго полека заострен сладолед конус, со точка 108 инчи зад квартал. Се разбира, тоа е опкружен со fuzzier област, наречена “делумна сенка”, каде што сончевата светлина се делумно блокиран. Целосно засенчена површина се нарекува “целосна сенка”. (Ова е латински збор за сенка. Чадор значи малку сенка на италијански јазик.) Ако лента една четвртина до крајот на тенок стап, и држете го во сонцето соодветно, може да се види овие различни области сенка.
Прашање: ако сте користеле пара наместо една четвртина, колку далеку од окото ќе треба да го држите за да ја блокирате целосната месечина од тоа око? Како различните растојанија се однесуваат на релативните големини на пара и четвртина? Нацртајте дијаграм кој ги прикажува двете конусни сенки.
Сега замислете дека сте во вселената, некои од далечина од земјата, гледајќи во сенка на Земјата. (Се разбира, може да се само навистина да се види тоа ако испукана облак од ситни честички и гледав кој од нив блеснаа во сончева светлина, а кои беа во мракот.) Јасно е сенка на земјата мора да биде конусна, исто како што од четвртина. И тоа исто така мора да биде слична на четвртина во техничка смисла, тоа мора да биде долга 108 земјата дијаметри! Тоа е затоа што поентата на конус е најдалечната точка на која земјата може да ги блокира сите сончева светлина, и односот на тоа растојание на дијаметар е определен со аголна големина на сонцето што го блокираш. Ова значи дека на конус е долга 108 земјата дијаметри, екстремната точка 864.000 милји од земјата.
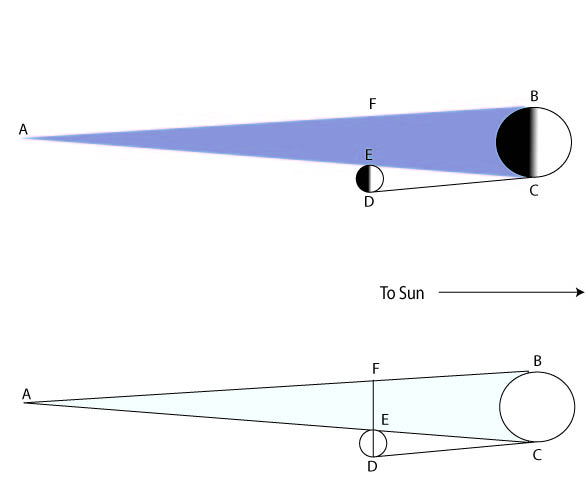
Сега, за време на целосно затемнување на Месечината, месечината се движи во овој конус на темнината. Дури и кога Месечината е сосема внатре во сенката, сè уште може да се види слабо, поради светлината расфрлана од атмосферата на Земјата. Со внимателно набљудување на Месечината за време на затемнувањето, и гледајќи како сенката на Земјата падна врз неа, Грците најдоа дијаметарот на конусната сенка на Земјата на растојание од месечината изнесува околу два и пол пати од сопствениот дијаметар на Месечината.
Забелешка: можно е да ја проверите оваа проценка или од фотографија на месечината која влегува во сенката на земјата, или, подобро, со вистинско набљудување на затемнувањето на Месечината.
Прашање: грците во овој момент ја знаеле големината на земјата (приближно сфера од 8.000 милји во дијаметар) и затоа големината на конусната сенка на земјата (должина 108 пати 8.000 милји). Тие знаеја дека кога месечината поминува низ сенката, дијаметарот на сенката на тоа растојание беше два и пол пати од дијаметарот на Месечината. Дали е тоа доволно информации за да дознаете колку е далеку Месечината?
Па, тоа им беше кажано дека месечината не беше подалеку од 108×8.000 = 864.000 милји, инаку месечината нема да помине низ сенката на земјата на сите! Но, од она што го кажавме досега, може да биде мала месечина од речиси 864.000 милји далеку, минувајќи низ таа последна малку сенка во близина на точка. Меѓутоа, толку мала месечина никогаш не може да предизвика затемнување на Сонцето. Всушност, како што добро знаеле Грците, месечината е иста очигледна големина на небото како и сонцето. Ова е суштинскиот факт што го користеле за да ја откријат растојанието на Месечината од земјата.
Тие го решат проблемот користејќи геометрија, конструирајќи ја сликата подолу. Во оваа бројка, фактот дека месечината и сонцето имаат иста привидна големина на небо значи дека аголот ECD е ист како и аголот EAF. Забележете сега дека должината FE е дијаметар на сенката на земјата на растојание од месечината, а должината ED е дијаметар на месечината. Грците пронајдоа со набљудување на затемнувањето на Месечината дека односот на FE во ED е 2,5 на 1, па гледајќи ги сличните рамнокраки триаголници FAE и DCE, заклучуваме дека AE е 2,5 пати поголема од EC, од која AC е 3,5 пати додека ЕК. Но, тие знаеја дека AC мора да биде должина од 108 дијаметар на земјата, а земајќи го дијаметарот на Земјата да биде 8.000 милји, најдалечната точка на конусната сенка, А, е 864.000 милји од Земјата. Од горенаведениот аргумент, ова е 3,5 пати подалеку од месечината, па растојанието до Месечината е 864.000/3.5 милји, околу 240.000 милји. Ова е во рамките на неколку проценти од вистинската бројка. Најголемиот извор на грешка е веројатно проценката на односот на големината на Месечината на онаа на сенката на Земјата како што минува низ неа.
Колку е далеку Сонцето?
Ова беше уште потешко прашање што го поставуваа грчките астрономи, и тие не го сторија тоа добро. Тие излегоа со многу генијален метод за мерење на далечината на сонцето, но се покажаа премногу тешки поради тоа што не можеа точно да го измерат важен агол. Сепак, од овој пристап научиле дека сонцето е многу подалеку од Месечината, а со тоа, бидејќи има иста привидна големина, мора да биде многу поголемо од месечината или од земјата.
Нивната идеја за мерење на дистанцата на сонцето беше многу едноставна во принцип. Тие, се разбира, знаеја дека месечината блеска со одраз на светлината на Сонцето. Затоа, тие размислувале, кога месечината се чини дека е точно половина полна, линијата од месечината до сонцето мора да биде токму нормална на линијата од месечината до набљудувачот (види ја сликата за да се убедиш во тоа). Значи, ако набљудувачот на земјата, при набљудување на половина месечина на дневна светлина, внимателно го мери аголот помеѓу правецот на месечината и насоката на сонцето, аголот α на сликата, тој треба да може да изгради долг тенок триаголник , со основната линија на линијата на Месечината, со агол од 90 степени на едниот крај, а од друга, и така го наоѓаат односот на растојанието на сонцето до растојанието на Месечината.
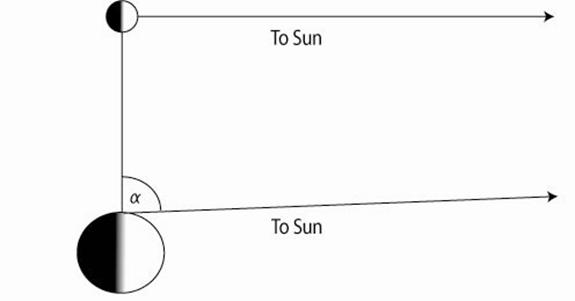
Проблемот со овој пристап е дека аголот α на испоставува да се разликуваат од 90 степени за околу една шестина од еден степен, премногу мали за да се измери точно. Првиот обид беше од Аристарх, кој се проценува на агол да биде 3 степени. Ова ќе ја стави на сонцето само пет милиони милји далеку. Сепак, тоа веќе ќе укажуваат на сонцето да биде многу поголема од Земјата. Тоа беше веројатно оваа реализација, што доведе Аристарх да укажуваат на тоа дека Сонцето, а не Земјата, е во центарот на универзумот. Најде најдобрите подоцна грчките обиди оддалеченост од сонцето да биде околу половина од правилната вредност (92 милиони милји).
Презентацијата тука е слична на онаа во Ерик Роџерс, Физика за истражувачки ум, Принстон, 1960 година.
Некои вежби поврзани со овој материјал се прикажани во белешките за физика 621.