Source: http://primes.utm.edu/notes/conjectures/

(Уште еден од ресурсите на Prime Pages)

Нов рекорд прост број: 2^74,207,281-1 со 22,338,618 бројки од Купер, Вольтман, Куровски, Блоссер и GIMPS (7 јан 2016).

Подолу се само неколку од многуте претпоставки во врска со прости броеви.

Претпоставка Голдбах: секој дури n> 2 е збир на две прости броеви.

Goldbach му напиша писмо на Ојлер во 1742 укажува на тоа дека секој цел број n> 5 е збир на три прости броеви.  Ојлер одговори дека ова е еквивалент на секој дури и n> 2 е збир на две прости броеви–ова е сега познат како претпоставка Голдбах е.  Шнитцель покажа дека претпоставка Голдбах е еквивалентно на секој цел број n> 17 е збир на три различни прости броеви.
Докажано е дека секој, дури и цел број е збир од најмногу шест прости броеви [Рамаре95] (претпоставка Голдбах сугерира два) а во 1966 година се покажа Чен секој доволно голем, па дури број е збир на главниот плус голем број со не повеќе од два главни фактори (P₂). Во 1993 година Синисало проверат претпоставка Голдбах за сите цели броеви помалку од 4^.10¹¹ [Синисало93]. Во поново време, Жан-Марк Дешуле, Јаник Саутер и Херман те Риле сте потврдиле ова до 10¹⁴ со помош на Креј C90 и разни работни станици. Во јули 1998 година, Јорг Рихштајн заврши проверката на 4^.10¹⁴ и се става листа на Шампионите Онлајн. Поновите работа од страна на Оливеира е Силва го продолжи ова на најмалку 4^.10¹⁷. Види [Рибенбојм95] и [Ванг84] за повеќе информации.

Чудно Голдбах проблем: секој чудно n> 5 е збир на три прости броеви.

Постигнат е значителен напредок во однос на ова, толку полесно случај на претпоставка Голдбах е. Во 1937 година Виноградов покажа дека ова е точно за доволно голем чудни броеви n. Во 1956 година покажа Бородзкин n > 3^14348907 доволно (тае изложувач ек 3¹⁵). Јован 1989 Чен и Ванг намали оваа врзани за 10⁴³⁰⁰⁰. Експонент се уште мора да се намали драматично пред да можеме да користат компјутери за да се грижи за сите мали предмети.

Секој парен број е разликата од две прости броеви.

Работата на Чен наведени во дискусијата на Голдбах претпоставка исто така, покажа дека секој парен број е разликата помеѓу премиерот и P₂.

За секој парен број 2n постојат бесконечно многу парови на последователни прости броеви кои се разликуваат од 2n.

Претпоставувал од Полигнак 1849.  Кога n = 1 ова е близнак прости броеви претпоставка. Тоа е лесно да се покаже дека за секој позитивен цел број m има парен број 2n, така што има повеќе од m парови на последователни прости броеви со разлика 2n.

Близнак прости броеви претпоставка: постојат бесконечно многу прости броеви близнаци.

Во 1919 Брун покажа дека збирот на реципрочни на близнаци прости броеви конвергира, како што тоа збирот B = (1/3 + 1/5) + (1/5 + 1/7) + (1/11 + 1/13) + (1/17 + 1/19) + … е постојана Брун.  B = 1.902160577783278…  Види влегувањето прости броеви речник на близнак прости броеви претпоставка.

Дали постојат бесконечно многу прости броеви на образецот n²+1?

Постојат бесконечно многу од формите n²+m² и n²+m²+1.  Поопшта форма на оваа претпоставка е ако a, b, c се релативно прости броеви, a е позитивен, a+b и c не се и дури, и b²-4ac не е совршен квадрат, тогаш постојат бесконечно многу прости броеви an²+bn+c [ХР79, стр19].

Бројот на Ферма прости броеви е конечен.

Харди и Рајт даде аргумент за оваа претпоставка во нивните добро познати фуснота [ХР79, стр15] која оди приближно како што следува.  Од страна на прост број теорема веројатноста дека еден случаен број n е прост број е најмногу a/log(n) за некои изборот на a.  Па се очекува бројот на Ферма прости броеви е најмногу збирот на a/log(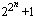) < a/2ⁿ, но оваа сума е a. Сепак, како Харди и Рајт белешка, бројките Ферма не се однесуваат “случајно” со тоа што се во парови релативно прости…

Е секогаш одличен помеѓу n² и (n+1)²?

Во 1882 година изјави Опперман pi(n²+n) > pi(n²) > pi(n²–n) (n>1), кој исто така се чини многу веројатно, но останува нејасна [Рибенбојм95, стр248].  И двете од овие претпоставки ќе го следат ако ние може да се покаже на претпоставка дека меѓу прости броеви интервал кон следните но се прост број p ек ќе ја повредени колена и постојаното пати (log p)².